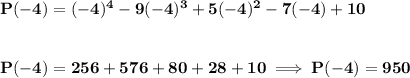Question

Tbh i got no clue how to do this i'd love some help

Use synthetic division and remainder theorem to find p(a).
P(x)=x^4-9x^3+5x^2-7x+10.
a= (-4)

Answer 1

so for P(a), to be P(-4), it simply means the argument takes the value of -4, namely x = - 4, and we can solve that for 0 and end up with a factor of x + 4 = 0.

so, the remainder theorem says that, P(a) gives us some value, say "r".

now if we divide P(x) by (x-a), the remainder from that division, either long division or synthetic doesn't matter, low and behold, is the same "r" we've got from P(a)!!!.

so, in this case we have P(-4), namely the division will be with the expression (x + 4) as you saw above, but we'll be using synthetic division, and the synthetic division uses the equality value, namely x = -4, so for the division we'll use the -4.

first off, we have to sort P(x) in descending order, P(x) = x⁴ - 9x³ + 5x² - 7x + 10, but but but, P(x) is already in descending order, so we're good to divide.

the synthetic division uses the sorted coefficients only, bear in mind that we "drop down the first coefficient" and start multiplying and adding from there.

`\bf \begin{array}rrrrrl -4&1&-9&5&-7&10\\ &&-4&52&-228&940\\ \cline{1-6} &\underset{\underset{dropped}{\qquad \uparrow }}{\qquad 1}&-13&57&-235&\boxed{950}&\leftarrow remainder \end{array}`

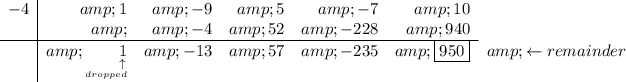
now according to the synthetic division, P(-4) is 950, is that true?

`\bf P(-4)=(-4)^4-9(-4)^3+5(-4)^2-7(-4)+10 \\\\\\ P(-4)=256+576+80+28+10\implies P(-4)=950`