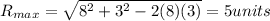Question

Given two vectors, one 8 units in length the other 3 units in length, explain why the maximum resultant of the two is a single vector 11 units in length and the minimum resultant of the two is a single vector 5 units in length.

Answer 1

Here two vectors are given of lengths

`\vec l_1 = 8 units`

`\vec l_2 = 3 units`

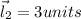
now let say the two vectors are inclined at some angle with each other

so the resultant is given as

`R = √(l_1^2 + l_2^2 + 2l_1 l_2 cos\theta)`

now plug in all values

`R = √(8^2 + 3^2 + 2(8)(3)cos\theta)`

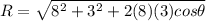
Now for maximum resultant the angle between two vectors must be ZERO degree

`R_(max) = √(8^2 + 3^2 + 2(8)(3)) = 11 units`

Now for minimum resultant the angle between two vectors must be 180 degree

`R_(max) = √(8^2 + 3^2 - 2(8)(3)) = 5 units`