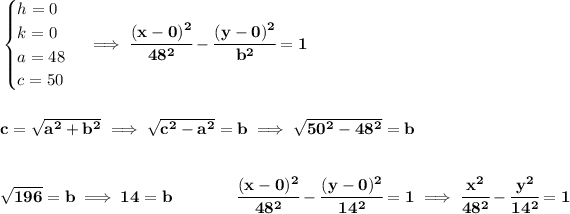bearing in mind that "a" is the length of the traverse axis, and "c" is the distance from the center to either foci.
we know the center is at (0,0), we know there's a vertex at (-48,0), from the origin to -48, that's 48 units flat, meaning, the hyperbola is a horizontal one running over the x-axis whose a = 48.
we also know there's a focus point at (50,0), that's 50 units from the center, namely c = 50.
![\bf \textit{hyperbolas, horizontal traverse axis } \\\\ \cfrac{(x- h)^2}{ a^2}-\cfrac{(y- k)^2}{ b^2}=1 \qquad \begin{cases} center\ ( h, k)\\ vertices\ ( h\pm a, k)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad √( a ^2 + b ^2)\\ \textit{asymptotes}\quad y= k\pm \cfrac{b}{a}(x- h) \end{cases} \\\\[-0.35em] \rule{34em}{0.25pt}](https://img.qammunity.org/2019/formulas/mathematics/college/n6o1zg2jhhuiofn0ocsvscooo75voyld4d.png)