Question

Dallas needs 1/4 liter of milk for a recipe , and there is 3/10 of a liter of milk left in the carton. How much is left after Dallas makes his recipe?

Answer 1

namely is just the difference of 3/10 - 1/4, since the denominators are 10 and 4, the LCD will then be 20.

`\bf \cfrac{3}{10}-\cfrac{1}{4}\implies \stackrel{\textit{using the LCD of 20}}{\cfrac{(2)3-(5)1}{20}}\implies \cfrac{6-5}{20}\implies \cfrac{1}{20}`

Answer 2

There are
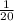`(1)/(20)` of milk left in the carton after Dallas makes his recipe.

Explanation:

If there are
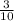`(3)/(10)` of milk before Dallas used it and
`(1)/(4)` after it, it means that we have to substact the quantities to know how much milk is left, so we have:

`(3)/(10)-(1)/(4)`

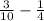
Now, to solve it, we have to find the least common denominator, that is the lower common multiple of the denominators, and if you see in the picture below, it is easy if we compare the multiples of the two numbers, so the least common denominator between 10 and 4 is 20, and now we can solve the substraction:

First we put in the denominator the LCD we found:

`(3)/(10)-(1)/(4)=\frac{}{20}`

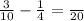
Then we take this LCD and divided it by 10 (the denominator of the first fraction) and then multiply it by 3, that is the numerator of the first fraction:

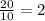`(20)/(10)=2` and 2 * 3 = 6

so we have:

`(3)/(10)-(1)/(4)=(6-)/(20)`

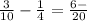
Then we do the same with the second fraction so
`(20)/(4)=5` and 5 * 1 = 5

and we have:

`(3)/(10)-(1)/(4)=(6-5)/(20)`

Finally we substract the numerators, and we have the answer:

`(6-5)/(20)=(1)/(20)`