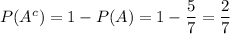Answer-
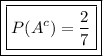
Solution-
Here,
Sample space = S = {Rome, Tokyo, Houston, Peru, Miami, Toronto, Canada}
So,
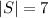
Event A = The randomly selected place is a city.
A = {Rome, Tokyo, Houston, Miami, Toronto}
So,
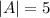
Hence,
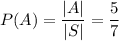
Then,
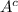 be the event that the randomly selected place is not a city, so
be the event that the randomly selected place is not a city, so