Answer:
√8, √10, √15
Explanation:
An irrational number can not be written in the form of
 ,
,
Where,
p and q are integers,
Such that q ≠ 0,
Also, a prime number inside square root is always an irrational number.
And, when we multiply an irrational number by a rational number the resultant number is also irrational.
While, when we multiply two different irrational numbers the result is also irrational.
∵ √4 = 2 =
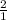 where, 2 and 1 are integers s. t. 1 ≠ 0,
where, 2 and 1 are integers s. t. 1 ≠ 0,
⇒ √4 is not irrational.
√8 = 2 × √2 = product of rational number and irrational number
⇒ √8 is irrational,
√10 = √5 × √2 = product of two different irrational numbers
⇒ √10 is irrational,
√15 = √3 × √5 = product of two different irrational numbers
⇒ √15 is irrational,
√36 = 4,
⇒ √36 is not irrational.