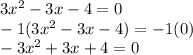Question

Using the quadratic formula, the solutions to a quadratic equation are given by (equation is in image)

Find the values of a, b and c
a =
b =
c =

Answer 1

a = -3

b = 3

c = 4

Explanation:

Let's do this the long way!

`x = (-3 \pm√(3^2 - 4 * (-3) * 4))/(2 * (-3))\\-6x = -3 \pm√(3^2 - 4 * (-3) * 4)\\-6x + 3 = \pm√(3^2 - 4 * (-3) * 4)\\(-6x + 3)^2 = 3^2 - 4 * (-3) * 4\\36x^2 - 36x + 9 = 9 + 48\\36x^2 - 36x - 48 = 0\\3x^2 - 3x - 4 = 0`

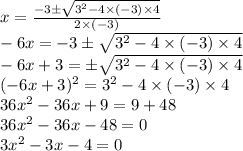
So a = 3, b = -3, and c = -4

HOWEVER:

When you look at the terms in the solution originally given, the are all the negatives of what we see here. That however makes sense, as we can simply multiply both sides of the equation to get the results they used:

`3x^2 - 3x - 4 = 0\\-1(3x^2 - 3x - 4) = -1(0)\\-3x^2 + 3x + 4 = 0`