Question

Gina is six years older than twice her cousin Noah's age. The sum of their ages is less than 36. What is the greatest age that Noah could be?

Answer 1

Noah's age represented as 'N' and Gina's age as '6 + 2N' results in the inequality '3N + 6 < 36'. Solving this, we find 'N < 10', meaning the greatest age Noah could be is 9 years old.

Step-by-step explanation:

To find the greatest age that Noah could be, we need to set up an inequality based on the information provided:

• Let N represent Noah's age.
• Then Gina's age is 6 + 2N (Gina is six years older than twice Noah's age).
• The sum of their ages is less than 36, so N + (6 + 2N) < 36.

Combining like terms and solving the inequality:

1. 3N + 6 < 36
2. 3N < 30
3. N < 10

Since the greatest integer less than 10 is 9, the greatest age Noah could be is 9 years old.

Answer 2

Given: Gina is six years older than twice her cousin Noah's age

Let the age of Noah be x years.

then,

Gina age be
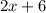`2x+6` years

Also, the sum of their ages is less than 36.

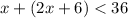`x+(2x+6)<36` or

x+2x+6<36 or [Combine like terms]

3x +6 <36

Subtract 6 from both sides of an equation:

3x+6-6<36-6 or

3x< 30

Divide both side by 3 we have;

x < 10

Therefore, the greatest age that Noah could be , 9 years old