Question

Need Help finding the composition of two rational functions. I attached a screenshot of the question i could use some help with

Answer 1

using (f ○ g )(x) = f(g(x))

f(g(x) =f(
`(1)/(x)`)

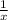substitue x =
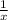`(1)/(x)` in f(x)

=
`(1)/(x)` /
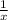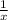`(1)/(x)` - 3 ×
`(x)/(x)`

=
`(1)/(1-3x)`

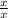
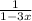
the denominator of f(g(x)) cannot be zero as this would make f(g(x)) undefined. Equating the denominator to zero and solving gives the value that x cannot be

solve 1 - 3x = 0 ⇒ - 3x = - 1 ⇒ x =
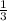`(1)/(3)` ← excluded value

domain is x ∈ (- ∞,
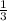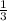`(1)/(3)`) ∪ (
`(1)/(3)`, + ∞ )