Answer: The measure of angle A is 60 degree.
Step-by-step explanation:
It is given that the Triangles A B E and D C E share vertex E. Angle B is 18 degrees. Angle C is 43 degrees. Angle D is 35 degrees.
According to angle sum property, the sum of angles of a triangle is always 180 degree.
In triangle CDE,
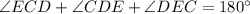
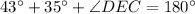
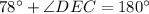

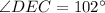
According to opposite vertical angle property.
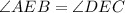
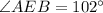
Use angle sum property is triangle ABE.
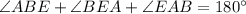
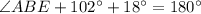
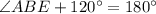
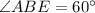
Therefore, the measure of angle A is 60 degree.