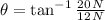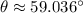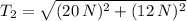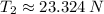Question

Please help thank you

Answer 1

`\theta \approx 59.036^(\circ)`,
`T_(2) \approx 23.324\,N`

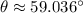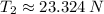
Step-by-step explanation:

First we build the Free Body Diagram (please see first image for further details) associated with the mass, we notice that system consist of a three forces that form a right triangle (please see second image for further details): (i) The weight of the mass, (ii) two tensions.

The requested tension and angle can be found by the following trigonometrical and geometrical expressions:

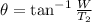`\theta = \tan^(-1) (W)/(T_(2))` (1)

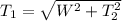`T_(1) = \sqrt{W^(2)+T_(2)^(2)}` (2)

Where:

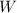`W` - Weight of the mass, measured in newtons.

`T_(1)`,
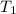`T_(2)` - Tensions from the mass, measured in newtons.

If we know that
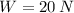`W = 20\,N` and
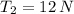`T_(2) = 12\,N`, then the requested values are, respectively:

`\theta = \tan^(-1) (20\,N)/(12\,N)`

`\theta \approx 59.036^(\circ)`

`T_(2) = \sqrt{(20\,N)^(2)+(12\,N)^(2)}`

`T_(2) \approx 23.324\,N`