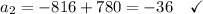Question

HELP! 15 POINTS!

MATH-


Find an explicit rule for the nth term of a geometric sequence where the second and fifth terms are -36 and 2304, respectively.

an = 9 • 4n
an = 9 • (-4)n + 1
an = 9 • 4n - 1
an = 9 • (-4)n - 1

Answer 1

an=9*(-4)^n-1

Explanation:

substitute n to 2 and we get a2=9*(-4)^2-1 a2=9*-4=-36

substitute n to 5 and we get a5=9*(-4)^5-1 a5=9*256=2304

Answer 2

It's pretty easy to go through the choices and none has a[2]=-36 and a[5]=2304. Something's probably wrong with the way the question is typed, but I will answer what's written.

`a_n = a + (n-1) d`

`a_2 = -36 = a + d`

`a_5 = 2304 = a + 4d`

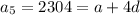
Subtracting,

`2340 = 3d`

`d = 2340/3 = 780`

`a = -36 - d = -36 - 780 = -816`

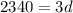
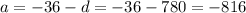
Answer: a[n] = -816 + 780(n-1) which is none of the above

Check:

`a_2 = -816 + 780= -36 \quad\checkmark`

`a_5 = -816 + 780(4) = 2304 \quad\checkmark`