Question

Megan tries to open a door, but she is unable to push at a right angle to the door. So, she pushes the door at an angle of 55º from the perpendicular. How much harder would she have to push to open the door just as fast as if she were to push it at 90º

Answer 1

Let say torque required to open the door when force is applied at 90 degree is given by T

`\tau = \vec r * \vec F`

`\tau = rFsin\theta`

`\tau = rFsin90 = rF`

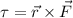
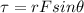
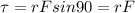
now if she is not able to apply force perpendicular but she can apply some harder force to open the door at 55 degree from perpendicular

now we can say

`\tau = rF'sin\theta`

`\tau = rF' sin(90 - 55)`

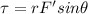
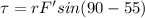
now we know that it requires same torque in order to open the door

so we will use the equation

`rF = rF'sin35`

`F' = (F)/(sin35) = 1.74 F`

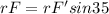
so it requires 1.74 times more force in this case