Question

Angles α and β are angles in standard position such that: α terminates in Quadrant II and sinα = 3/5, β terminates in Quadrant I and cosβ = 4/5 Find cos(α + β).

Answer 1

We are given

Angles α and β are angles in standard position

and

α terminates in Quadrant II

β terminates in Quadrant I

and we have

`sin(\alpha)=(3)/(5)`

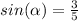
we can use triangle and find cos(α)

we get

`cos(\alpha)=-(4)/(5)`

and we have

`cos(\beta)=(4)/(5)`

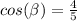
we can draw triangle

`sin(\beta)=(3)/(5)`

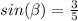
now, we can use formula

`cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)`

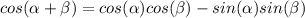
now, we can plug values

`cos(\alpha+\beta)=-(4)/(5)* (4)/(5)-(3)/(5)* (3)/(5)`

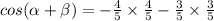
now, we can simplify it

`cos(\alpha+\beta)=-(16)/(25)-(9)/(25)`

`cos(\alpha+\beta)=-((16+9))/(25)`

`cos(\alpha+\beta)=-((16+9))/(25)`

`cos(\alpha+\beta)=-(25)/(25)`

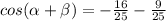
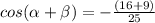
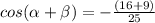
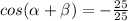
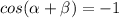`cos(\alpha+\beta)=-1`...............Answer