Question

the order or arrangement of items doesnt matter when you are determining the combination. True or False?

Answer 1

True.

If you have
`n` objects, the most common and important combinatorics elements you have are:

• Permutations: you use every element, and the point is: "how do you order them?".
• Dispositions: you choose a subset of
  `k<n` elements, and consider a specific position for each element in the subset. So, you're asking "how many ordered subsets of
  `k` elements can I get from my
  `n`-elements set?
• Combinations: you choose a subset of
  `k<n` elements. So, you're asking "how many subsets of
  `k` elements can I extract from my
  `n`-elements set?

Here are some examples: if you start from the set
`\{1,2,3\}`, all the possible permutations are

`\{1,2,3\},\ \{1,3,2\},\ \{2,1,3\}, \{2,3,1\}, \{3,1,2\}, \{3,2,1\}`

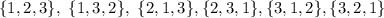
All the possible dispositions, choosing the subset cardinality
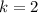`k=2`, are

`\{1,2\},\ \{2,1\},\ \{1,3\},\ \{3,1\},\ \{2,3\},\ \{3,2\}`

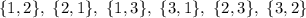
So, as you can see, the order matters, because
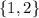`\{1,2\}` and
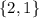`\{2,1\}` are not the same element.

Finally, the combinations (still with
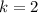`k=2`) are

`\{1,2\},\ \{1,3\},\ \{2,3\}`

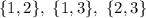
Because now the order doesn't matter, and thus
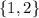`\{1,2\}` and
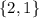`\{2,1\}` are seen as the same element.