Question

Find the intercepts and relative extrema for the graph of each function.

1. f(x)=1/4(x+2)(x-1)^2

2. h(x)=2x^3+5x^2-25x

Answer 1

Definition:

x -intercept : The point where the graph crosses the x-axis

Substitute in y=0 and solve for x

y-intercept : The point where the graph crosses the y-axis

Substitute in x=0 and solve for f(x) or y

1.

Given the function f(x) =
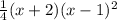`(1)/(4)(x+2)(x-1)^2` .....[1]

to find x-intercept;

substitute y= 0 in equation [1];

`(1)/(4)(x+2)(x-1)^2=0`

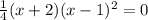
⇒ x+2 = 0 and
`(x-1)^2 =0`

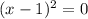
⇒ x =-2 and x= 1

Therefore, the x-intercept are; (-2,0) and (1 ,0)

Similarly, for y-intercept

Substitute x=0 in [1] to solve for y;

`y=f(x)=(1)/(4) (0+2)(0-1)^2`

⇒
`y = (1)/(4)(2)(-1)^2`

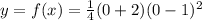
Simplify;

y =
`(1)/(2)`

therefore, the y-intercept is, (0,
`(1)/(2)`)

To find the relative extrema for the function f(x) =
`(1)/(4)(x+2)(x-1)^2`;

Relative Extrema states that when the graph is turning around then there must be a horizontal tangent at that point, also we can say that the derivative value will be zero at that point, because a horizontal tangent has slope equal to 0.

As you can see in the Figure 1

Relative extrema of the function f(x) are (-1,1) and (1,0)

2.

Given the function h(x) =
`2x^3+5x^2-25x` .....[2]

to find x-intercept;

substitute y= 0 in equation [2];

`2x^3+5x^2-25x=0` or

`x(2x^2+5x-25)=0` or

`x(x+5)(2x-5)=0`

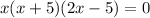
Simplify:

x =0, x=-5 and
`x= (5)/(2)`

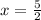
Therefore, the x-intercept are; (0,0), (-5,0) and (
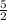`(5)/(2)`,0)

Similarly, for y-intercept

Substitute x=0 in [2] to solve for y=h(x);

h(x) =
`2(0)^3+5(0)^2-25(0)`

h(x) =0

therefore, the y-intercept is, (0,0)

To find the relative extrema for the function h(x) =
`2x^3+5x^2-25x`

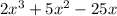
Relative Extrema states that when the graph is turning around then there must be a horizontal tangent at that point, also we can say that the derivative value will be zero at that point, because a horizontal tangent has slope equal to 0.

As you can see in the Figure 2

Relative extrema of the function h(x) are (-3.038, 66.019) and (1.371, -19.723)