Question

Suppose you have 48 feet of fencing to enclose a rectangular dog pen. The function A = 24x-x2, where x = width, gives you the area of the dog pen in square feet. What width gives you the maximum area? What is the maximum area?

Answer 1

We are given

`A=24x-x^2`

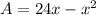
where

x is width of rectangle

A is area of rectangle

Since, we have to maximize it

so, we will find it's derivative

and then we can set it to 0

and then we can solve for x

`A'=24* 1-2x`

`A'=24-2x`

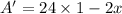
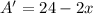
now, we can set it to 0

and then we can solve for x

`A'=24-2x=0`

`x=12`

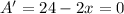
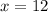
So, width is 12 feet

Maximum area:

we can plug x=12

`A=24(12)-(12)^2`

`A=144ft^2`

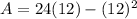
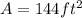
So, the maximum area is

`=144ft^2`................Answer