Answer:
The inequality will be:
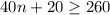
Tom must schedule at least 6 full-time employees.
Explanation:
Each full-time employee works 40 hours per week.
If the number of full-time employees is
 , then
, then
 number of full-time employees work
number of full-time employees work
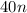 hours per week.
hours per week.
Tom has one part-time employee who works 20 hours per week.
So, the total hours worked by all employees
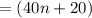 hours.
hours.
Given that, all his employees will work at least 260 person-hours per week.
So, the inequality will be:
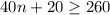
Solving the above inequality.....
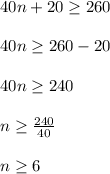
So, Tom must schedule at least 6 full-time employees.