Question

The base of pyramid A is a rectangle with a length of 10 meters and a width of 20 meters. The base of pyramid B is a square with 10-meter sides. The heights of the pyramids are the same. The volume of pyramid A is twice that of pyramid A, the new volume of pyramid B is the volume of pyramid B.If the height of pyramid B increases to the volume of pyramid A.

Answer 1

The volume of pyramid A is twice of pyramid B and if the height of pyramid B increased to twice that of pyramid A, the new volume of pyramid B is the equal to the volume of pyramid A.

Explanation:

Given information:

Pyramid A: Rectangular base of 10×20.

Pyramid B: Square base of 10×10.

It is given that

The volume of a pyramid is the heights of the pyramids are the same.

Let the height of both pyramids be h.

`V=(1)/(3)Bh`

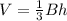
Where, B is base area and h is height of the pyramid.

The volume of Pyramid A is

`V_A=(1)/(3)(10* 20)h`

`V_A=(200)/(3)h`

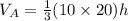
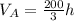
The volume of Pyramid B is

`V_B=(1)/(3)(10* 10)h`

`V_B=(100)/(3)h`

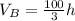
We conclude that,

`(200)/(3)h=2* (100)/(3)h`

`V_A=2* V_B`

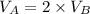
It means the volume of pyramid A is twice of pyramid B.

Now, the height of pyramid B increased to twice that of pyramid A.

Let the height of pyramid B is 2h and height of pyramid a is h.

`V_A=(1)/(3)(10* 20)h`

`V_A=(200)/(3)h`

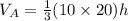
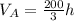
The volume of Pyramid B is

`V_B=(1)/(3)(10* 10)2h`

`V_B=(200)/(3)h`

`V_B=V_A`

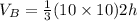
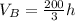
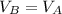
Therefore the volume of pyramid A is twice of pyramid B and if the height of pyramid B increased to twice that of pyramid A, the new volume of pyramid B is the equal to the volume of pyramid A.

Answer 2

The volume of rectangle pyramid can be calculated using formula:

`V_(pyramid)=(1)/(3)\cdot \text{length}\cdot \text{width}\cdot \text{height}.`

1. If the base of pyramid A is a rectangle with a length of 10 meters and a width of 20 meters, then

`V_(A)=(1)/(3)\cdot 10\cdot 20\cdot H_A=(200)/(3)H_A.`

2. If the base of pyramid B is a square with 10-meter sides, then

`V_(B)=(1)/(3)\cdot 10\cdot 10\cdot H_B=(100)/(3)H_B.`

3. If heights
`H_A,\ H_B` are the same, you can see that

`V_(A)=2V_(B).`

Answer 1: twice (2 times)

If
`H_B=2H_A,` then

`V_(B)=(100)/(3)H_B=(100)/(3)\cdot 2H_A=(200)/(3)H_A=V_(A).`

Answer 2: the same