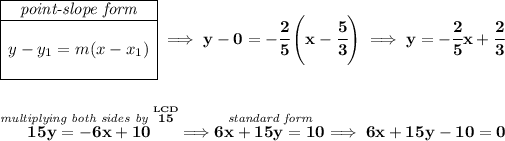Question

The line y =3x-5 meet x-axis at the point M.

The line 3y+2x=2 meets y-axis at point N.
Find the equation of the line joining M and N in the form ax + by + c = 0 where: a,b,c are integers.

Answer 1

y = 3x - 5 meets the x-axis at the x-intercept, and that happens when y = 0

`\bf \stackrel{y}{0}=3x-5\implies 5=3x\implies \cfrac{5}{3}=x~\hspace{5em}\stackrel{M}{\left( (5)/(3),0 \right)}`

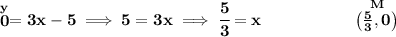
3y + 2x = 2, meets the y-axis when x = 0, and that'd be the y-intercept

`\bf 3y+2(\stackrel{x}{0})=2\implies 3y=2\implies y=\cfrac{2}{3}~\hspace{5em}\stackrel{N}{\left( 0,(2)/(3) \right)}`

so let's find the equation of the line with points M and N in standard form, bearing in mind that

standard form for a linear equation means

• all coefficients must be integers, no fractions

• only the constant on the right-hand-side

• all variables on the left-hand-side, sorted

• "x" must not have a negative coefficient

`\bf M(\stackrel{x_1}{(5)/(3)}~,~\stackrel{y_1}{0})\qquad N(\stackrel{x_2}{0}~,~\stackrel{y_2}{(2)/(3)}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{~~(2)/(3)-0~~}{0-(5)/(3)}\implies \cfrac{2}{3}\cdot -\cfrac{3}{5}\implies -\cfrac{2}{5}`

`\bf \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-0=-\cfrac{2}{5}\left( x-\cfrac{5}{3} \right)\implies y=-\cfrac{2}{5}x+\cfrac{2}{3} \\\\\\ \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{15}}{15y=-6x+10}\implies \stackrel{\textit{standard form}}{6x+15y=10}\implies 6x+15y-10=0`