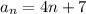Question

Find the simplest form of the general term for the sequence 11, 15, 19, 23, . . .

A. 4n + 7
B. 8n + 3
C. 8n + 2
D. 10n + 1

Answer 1

The answer is A.

This is because it is the only general term which works for every term in the sequence.

Answer 2

Answer:
`a_n=4n+7`

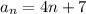
Explanation:

We are given a sequence 11, 15, 19, 23, . . . which shows a arithmetic progression having common difference d= 15-11=4

The First term a=11

We know that in Arithmetic Progression , the nth term of A.P is given by :-

`a_n=a+d(n-1)`

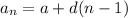
Put the values of a and d in the above equation.

`a_n=11+4(n-1)\\\\\Rightarrow\ a_n=11+4n-4\\\\\Rightarrow\ a_n=4n+7`

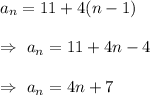
Hence, the simplest form of the general term for the given sequence:

`a_n=4n+7`