Question

A person who weighs 800N on the earths surface will weigh 200N at what height above the earth

Answer 1

Answer: 6,400 km

Step-by-step explanation:

The weight of a person is given by:

`W=mg`

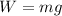
where m is the mass of the person and g is the acceleration due to gravity. While the mass does not depend on the height above the surface, the value of g does, following the formula:

`g=(GM)/(r^2)`

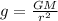
where

G is the gravitational constant

M is the Earth's mass

r is the distance of the person from the Earth's center

The problem says that the person weighs 800 N at the Earth's surface, so when r=R (Earth's radius):

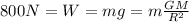`800 N= W=mg=m (GM)/(R^2)` (1)

Now we want to find the height h above the surface at which the weight of the man is 200 N:

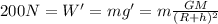`200 N = W' = mg' = m (GM)/((R+h)^2)` (2)

If we divide eq.(1) by eq.(2), we get

`(800 N)/(200 N)=(W)/(W')=((R+h)^2)/(R^2)`

`4=((R+h)^2)/(R^2)`

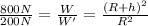
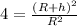
By solving the equation, we find:

`4R^2 = (R+h)^2=R^2+2Rh+h^2\\h^2 +2Rh-3R^2 =0`

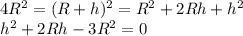
which has two solutions:

`h=-3R` --> negative solution, we can ignore it

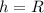`h=R` --> this is our solution

Since the Earth's radius is
`R=6.4\cdot 10^6 m`, the person should be at
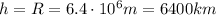`h=R=6.4\cdot 10^6 m=6400 km` above Earth's surface.