Question

The figures below are made out of circles, semicircles, quarter circles, and a square. Find the area and the perimeter of each figure and give your answers as a completely simplified exact value in terms of π (no approximations).

Answer 1

Area of the shaded region = 16(π - 2) in²

Perimeter of the shaded region = 4(π +
`2√(2)`) in

Explanation:

Since, BDC is a quarter of the circle with radius = 8 in.

Area of the quarter of the circle =
`(1)/(4)(\pi)(r)^2`

=
`(1)/(4)(64)\pi`

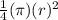
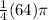
= 16π in²

Area of ΔBCD =
`(1)/(2)(\text{Base})(\text{Height})`

=
`(1)/(2)(8)(8)`

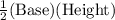
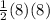
= 32 in²

Since, area of the shaded part = Area of quarter of the circle - Area of triangle BCD

= (16π - 32)

= 16(π - 2) in²

Therefore, area of the shade region = 16(π - 2) in²

Similarly, length of arc BD =
`(1)/(4)(2\pi r)`

=
`(8\pi )/(2)`

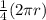
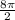
= 4π in.

Length of the diagonal of a square = (Side)√2

= 8√2 in

Perimeter of the shaded region = Length of arc BD + Length of diagonal BD

= 4π + 8√2

= 4(π + 2√2) in.