Question

Using rigid motion, which statement is true about the triangles? △ABC is congruent to △DEF . △ABC is congruent to △FDE . △ABC is congruent to △FED The triangles are not congruent. Two triangles A B C and D E F are given on a coordinate plane. Triangle A B C has vertices A at begin ordered pair negative 1 comma negative 2 comma, B at begin ordered pair negative 6 comma negative 1 end ordered pair, C at begin ordered pair negative 5 comma negative 5 end ordered pair. Triangle D E F has vertices D at begin ordered pair 1 comma negative 2 end ordered pair, E at begin ordered pair 6 comma negative 1 end ordered pair, and F at begin ordered pair 5 comma negative 5 end ordered pair.

Answer 1

△ABC is congruent to △DEF

Explanation:

△DEF is a reflection of △ABC across the y-axis. (Each x-coordinate is negated.)

_____

Comment on presentation

This would be much easier to answer if you would use a conventional representation of ordered pairs:

... (-1, -2) instead of "begin ordered pair negative 1 comma negative 2 end ordered pair"

Answer 2

The correct option is 1. △ABC is congruent to △DEF.

Explanation:

From the given information it is clear that the vertices of △ABC are A(-1,-2), B(-6,-1) and C(-5,-5).

The vertices of △DEF are D(1,-2), E(6,-1), F(5,-5).

Plot all these points on a coordinate plan. From the below graph it is clear that the △ABC is mirror image of △DEF across y-axis. The relation between coordinates of △ABC and △DEF is defined as

`(x,y)\rightarrow (-x,y)`

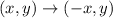
It means the graph △ABC reflect cross the y-axis to get △DEF.

Since reflection is a rigid transformation, therefore the size and shape of △ABC and △DEF are same and △ABC is congruent to △DEF.