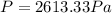Answers:
1. Firstly, we have to define that Pressure
 is Force applied
is Force applied
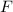 per unit area
per unit area
 . It is mathematically expressed as follows:
. It is mathematically expressed as follows:
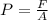 (1)
(1)
The unit of P is Pascal (Pa) which is equivalent to
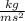 and also equivalent to
and also equivalent to
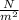
There is also another expression of the Pressure in which it is dependent on the density
 of the liquid, the height
of the liquid, the height
 of the container and the gravity force
of the container and the gravity force
 :
:
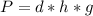 (2)
(2)
In this problem the liquid is water, and its known density is approximately:

So, we have to substitute the values in equation (2) to obtain the pressure (Being careful with the units):
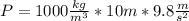
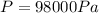
Then, we have to substitute this value in equation (1) and clear
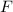 :
:
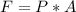
Finally:
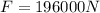
2. For this problem, we will use equation (1) to find the Pressure. We already know the area
 and the force exerted by water in the container
and the force exerted by water in the container
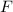 :
:
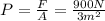

3. In this case, equation (2) is the perfect way to find the hydrostatic pressure at any point at the bottom of the tank (be careful with the units):
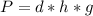


4. In this case, it's important to know that in fluids (in this case the water) the higher the fluid is, the lower the pressure. Then, if
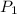 and
and
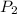 are the respective pressures at the heights
are the respective pressures at the heights
 and
and
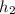 , and knowing that the water density and the gravity force in this case are constants, we can use the following expression to solve this problem:
, and knowing that the water density and the gravity force in this case are constants, we can use the following expression to solve this problem:
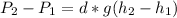 (3)
(3)
Where:
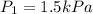 at
at

Note that

And
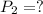 is unknown at a given height
is unknown at a given height

Then, we have to substitute the values in equation (3) to find
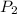 :
:
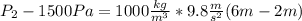
Finally:
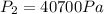
5. In this case we have the area
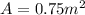 and the mass of the piston
and the mass of the piston
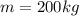 , and we need to know the pressure
, and we need to know the pressure
 .
.
We will use equation (1):
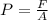
But, do you remember that above we stated that pressure is the force applied over an area?
Well, in this case we will use the following equation, in which the gravity force and the mass of a body are involved, to find
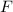 :
:
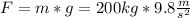
Then:
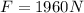
Now we can finally calculate
 :
: