Question

In the regular nonagon shown, what is the measure of angle x?

a
36°
b
40°
c
45°
d
60°

Answer 1

180-140=40

b is the answer

Answer 2

Option B.

Explanation:

A nonagon has 9 vertices. So, the number of exterior angles is 9.

We know that sum of exterior angles of any polygon is 360 degrees. So,

Sum of exterior angles of a nonagon = 360 degrees

The measures of all exterior angles of regular nonagon are same.

We need to find the measure of an exterior angle.

The measure of an exterior angle of a regular polygon is

`\text{Exterior angle}=\frac{360^\circ}{\text{Number of vertices}}`

`x^\circ=(360^\circ)/(9)`

`x^\circ=40^\circ`

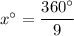
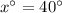
Therefore, the correct option is b.