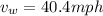Question

A plane travels at a speed of 205mph in still air. Flying with a tailwind, the plane is clocked over a distance of 1000 miles. Flying against a headwind, it takes 2 hours longer to complete the return trip. What was the wind velocity? (Round your answer to the nearest tenth.)

Answer 1

While plane is moving under tailwind condition it took time "t"

so here we will have

`t = (d)/(v_(net))`

here net speed of the plane will be given as

`v_(net) = v + v_w`

`t = (1000)/(205 + v_w)`

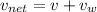
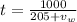
similarly when it moves under the condition of headwind its net speed is given as

`v_(net) = v - v_w`

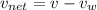
now time taken to cover the distance is 2 hours more

`t + 2 = (1000)/(205 - v_w)`

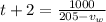
now solving two equations

`(1000)/(205 + v_w) + 2 = (1000)/(205 - v_w)`

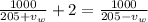
solving above for v_w we got

`v_w = 40.4 mph`