Question

There are some nickels, dimes, and quarters in a large piggy bank. For every 2 nickels there are 3 dimes. For every 2 dimes there are 5 quarters. There are 500 coins in total.

a. How many nickels, dimes, and quarters are in the piggy bank? Explain you reasoning.

b. How much are the coins in the piggy bank worth?

Answer 1

Answer: a) Number of nickels, dimes, and quarters are 80, 120, 300 respectively.

b) The coins are worth of 91 dollars i.e. $91 in the piggy bank.

Step-by-step explanation:

Since we have given that

For every 2 nickels there are 3 dimes ,

So, their ratio will be 2:3

and for every 2 dimes there are 5 quarters.\,

So, their ratio will be 2:5

Now, we'll first find the ratio of nickles to dimes to quarters i.e.

Nickle Dimes Quarters

2 3

2 5

So, it becomes ,

Nickle : Dimes : Quarters

2×2 : 3×2 : 3×5

4 : 6 : 15

Now, let the number of nickle be 4x

Let the number of dimes be 6x

Let the number of quarters be 15x

According to question,

`4x+6x+15x=500\\\\25x=500\\\\x=(500)/(25)=20`

So, number of nickels is given by

`4x=4* 20=80`

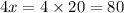
Number of dimes is given by

`6x=4* 20=120`

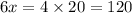
Number of quarters is given by

`15x=4* 20=300`

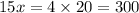
As we know that

`1\ nickel=5\ cents\\\\1\ dime=10\ cents\\\\1\ quarter=25\ cents`

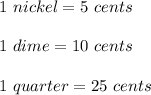
So, According to our question, we get

`80* 5+120* 10+300* 25=400+1200+7500=9100\ cents\\\\1\ cent=0.01\ dollar\\\\9100\ cents=9100* 0.01\ dollars=91\ dollars.`

Hence,

a) Number of nickels, dimes, and quarters are 80, 120, 300 respectively.

b) the coins are worth of 91 dollars i.e. $91 in the piggy bank.