Question

Marielle’s painting has the dimensions shown (Painting Width = 18 inches, Painting Length = 24 inches). The school asks her to paint a larger version that will hang in the cafeteria. The larger version will be twice the width and twice the height. Is the area of the original painting proportional to the area of the larger painting? If so, what is the constant proportionality?

Answer 1

Find out the what is the constant proportionality .

To prove

Formula

Area of rectangle = Length × Breadth

As given

Marielle’s painting has the dimensions shown (Painting Width = 18 inches, Painting Length = 24 inches).

Area of the original painting = 18 × 24

= 432 inches²

As given

The school asks her to paint a larger version that will hang in the cafeteria.

The larger version will be twice the width and twice the height.

Length of the larger version painting = 2 × 18

= 36 inches

Breadth of the larger version painting = 2 × 24

= 48 inches

Now area of the larger version painting = 36 × 48

= 1728 inches²

As given

The area of the original painting proportional to the area of the larger

painting .

Thus

`Area\ of\ original\ painting\ \propto\ Area\ of\ larger\ painting`

`Area\ of\ original\ painting\ = k* \ Area\ of\ larger\ painting`

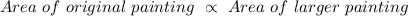
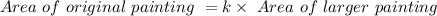
Where k is the constant of proportionality

Putting the value

432 = k × 1728

`k = (1728)/(432)`

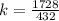
k = 4

The constant proportionality is 4 .

Hence proved