Question

Simplify the rational expression. State any restrictions on the variable. t^2-4t-32/t-8

Answer 1

The simplest form of
`(t^2-4t-32)/(t-8)` is t+4.

Explanation:

We are given an expression
`(t^2-4t-32)/(t-8)`.

Factorizing the numerator such that the factors when multiplied give a product of -32 and when added give a result of -4:

`(t^2-4t-32)/(t-8)`

`=(t^2-8t+4t-32)/(t-8)`

`= (t(t-8)+4(t-8))/(t-8)`

`=((t+4)(t-8))/(t-8)`

`= t+4`

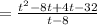
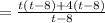
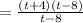
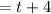
Since the denominator is
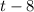`t-8` in this expression, therefore
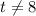`t\\eq 8` or it will be equal to zero which will make the overall value of the fraction undefined.

Answer 2

1. Factor the expression
`t^2-4t-32:`

`t^2-4t-32=(t-8)(t+4).`

2. Since
`t-8` is placed in the denominator of the given expression, then
`t\\eq 8.`

3. Now the expression can be simplified:

`(t^2-4t-32)/(t-8)=((t-8)(t+4))/(t-8)=t+4.`