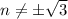ANSWER
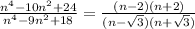
For
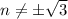
Step-by-step explanation
We have
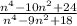
This is very easy to simplify. We shall look at the two expressions from a quadratic trinomial perspective.
We rewrite the rational expression to obtain;
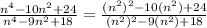
We can now see that both the numerator and denominator are quadratic trinomials in
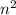 .
.
We split the middle terms as follows;
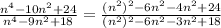
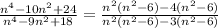
We factor further to obtain;
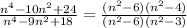
We now cancel out common factors to get;
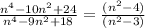
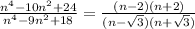
For