Question

I don't know how to do this or what i'm doing plz help

Answer 1

recalling that d = rt, distance = rate * time.

we know Hector is going at 12 mph, and he has already covered 18 miles, how long has he been biking already?

`\bf \begin{array}{ccll} miles&hours\\ \cline{1-2} 12&1\\ 18&x \end{array}\implies \cfrac{12}{18}=\cfrac{1}{x}\implies 12x=18\implies x=\cfrac{18}{12}\implies x=\cfrac{3}{2}`

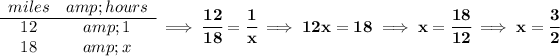
so Hector has been biking for those 18 miles for 3/2 of an hour, namely and hour and a half already.

then Wanda kicks in, rolling like a lightning at 16mph.

let's say the "meet" at the same distance "d" at "t" hours after Wanda entered, so that means that Wanda has been traveling for "t" hours, but Hector has been traveling for "t + (3/2)" because he had been biking before Wanda.

the distance both have travelled is the same "d" miles, reason why they "meet", same distance.

`\bf \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ Hector&d&12&t+(3)/(2)\\[1em] Wanda&d&16&t \end{array}\qquad \implies \begin{cases} \boxed{d}=(12)\left( t+(3)/(2) \right)\\[1em] d=(16)(t) \end{cases}`

`\bf \stackrel{\textit{substituting \underline{d} in the 2nd equation}}{\boxed{(12)\left( t+(3)/(2) \right)}=16t}\implies 12t+18=16t \\\\\\ 18=4t\implies \cfrac{18}{4}=t\implies \cfrac{9}{2}=t\implies \stackrel{\textit{four and a half hours}}{4(1)/(2)=t}`