Question

A population of insects grows exponentially, as shown in the table. Suppose the increase in population continues at the same rate.

What is the insect population at the end of week 11?

Round to the nearest whole number.

Answer 1

A population of insects grows exponentially, as shown in the table. Suppose the increase in population continues at the same rate.

from the given table

when x=0 , y=20

when x= 1 , y = 30

We use this information to find exponential growth equation

General form of exponential growth is

`y=a(b)^x`

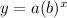
WE plug in the given values and find out value of a and b

when x=0 , y=20

`20=a(b)^0`

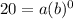
20 = a

Now we find out b

when x= 1 , y = 30

`30=20(b)^1`

divide both sides by 20

`(3)/(2) = b`

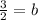
So exponential function becomes

`y=20((3)/(2))^x`

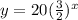
Now we find the insect population at the end of week 11

We plug in 11 for x

`y=20((3)/(2))^x`

`y=20((3)/(2))^11= 1729.951171875`

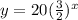
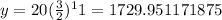
Round the answer to nearest whole number

1730 is the insect population at the end of week 11