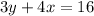Question

PLEASE HELP!! URGENT!!!! UNIT TEST!!!!

what is the equation of a line that is perpendicular to -3x + 4y = 4 and passes through the point (4,0)

Answer 1

y = -4/3x + 16/3 or 4x + 3y = 16

Explanation:

We know that the standard form of equation for a line is:

`y = mx +c` where
`m` is the slope of the line and
`c` is the y-intercept.

So writing the given equation in the standard form:

`y = (3)/(4) x+1`

According to this equation, the slops (m) is 3/4. So the slope of line perpendicular to this would be negative reciprocal of 3 i.e. -4/3.

Putting the value of the slope and the given point to find the y-intercept:

`y=mx+c`

`0= -(4)/(3) (4)+c`

`c = (16)/(3)`

Therefore, the equation of line perpendicular to -3x + 4y = 4 which passes through the point (4,0) is
`y = (-4)/(3)x+ (16)/(3)` or 4x + 3y = 16.

Answer 2

`y=-(4)/(3)x+(16)/(3)`

Or

`3y+4x=16`

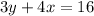
EXPLANATION

Let us find the gradient of the line:

`-3x+4y=4` by rewriting it in the slope intercept form.

`\Rightarrow 4y=3x+4`

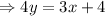
We divide through by 4 now;

`\Rightarrow y=(3)/(4)x+1`

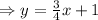
This is now in the form;

`y=mx+c`

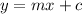
where

`m=(3)/(4)` is he slope.

This implies that the slope of the line that is perpendicular to this line will be the negative reciprocal of
`m=(3)/(4)` .

Thus the perpendicular line has slope,

`m=(-1)/((3)/(4))= -(4)/(3)`.

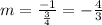Let the perpendicular line have equation,

`y=mx+c`

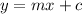
When we substitute the slope we have;

`y=-(4)/(3)x+c`

We substitute the point.
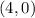`(4,0)` to find c.

`0=-(4)/(3)(4)+c`

`0=-(16)/(3)+c`

`(16)/(3)=c`

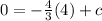
We substitute c to obtain;

`y=-(4)/(3)x+(16)/(3)`

Or

`3y+4x=16`