Question

A roller of radius 12.5 cm turns at 14 revolutions per second. What is the linear velocity of the roller in meters per second?

Answer 1

12.5 times 14 and convert to meters its 1.75 meters per second

Answer 2

Linear velocity of the roller, v = 11 m/s

Step-by-step explanation:

It is given that,

Radius of roller, r = 12.5 cm = 0.125 m

Angular velocity of the roller,
`\omega=14\ rev/s`

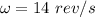
Firstly, we will convert revolution per second to radian per second i.e.

Angular velocity,
`\omega=87.96\ rad/s`

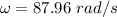
We need to find the linear velocity of the roller. It can be calculated by taking the product of angular velocity and the radius of roller.

`v=r* \omega`

`v=0.125\ m* 87.96\ rad/s`

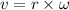
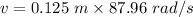
v = 10.995 m/s

or

v = 11 m/s

So, the linear velocity of the roller is 11 m/s. Hence, this is the required solution.