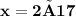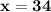Question

The sum of two numbers is 51 and the greater number is twice the smaller number. Find the numbers. a) set up the variables Let _______ represent the first number Then _______ will represent the second number. b) What is the equation that represents the above situation? c) Solve the equation.

Answer 1

`\tt{34~and ~17 }`

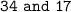
Explanation:

let the first number is =x

second number is =y

The sum of two numbers is 51 =x+y=51•••{1}

the greater number is twice the smaller number= x=2y••••••••{2}

According to the question,

`\bold{ x+y=51 }`

`\bold{2y+y=51 }`
`\because{ (x=2y ) }`

`\bold{ 3y=51 }`

`\bold{ y=(51)/(3) }`

`\boxed{\blue{y=17 } }`

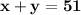
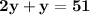
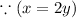
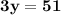
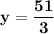
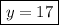
NOW put the value y in equation {2}

we get that,

`\bold{ x=2×17 }`

`\bold{ x=34 }`

Answer 2

• 34 and 17

Explanation:

a) set up the variables

Let x represent the first number Then y will represent the second number.

b) What is the equation that represents the above situation?

• x = 2y
• x + y = 51

c) Solve the equation.

Substitute x in the second equation and solve for y:

• x + y = 51
• 2y + y = 51
• 3y = 51
• y = 51/3
• y = 17

Then find x

• x = 2y = 2*17 = 34