Question

What are the real roots of this equation?

12/x-6+x=3+8x/x-6

A) x = 6
B) x = 7.04 and x = 1.095
C) x = 15 and x = 2
D) x = 15

Answer 1

The correct answer is
`x=15\:or\:x=2`

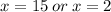
Step-by-step explanation

We have the equation;

`(12)/(x-6)+x=3+ (8x)/(x-6)`

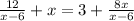
We multiply through by the least common multiple, which is
`(x-6)`.

This gives us;

`(x-6) * (12)/(x-6)+x(x-6)=3(x-6)+ (8x)/(x-6) * (x-6)`

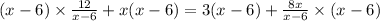
We simplify to obtain;

`12+x(x-6)=3(x-6)+ 8x`

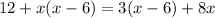
We now expand to obtain;

`12+x^2-6x=3x-18+ 8x`

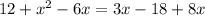
We rewrite the above equation as a quadratic equation in
`x`.

This implies that

`x^2-6x-3x-8x+12+18=0`

This simplifies to;

`x^2-17x+30=0`

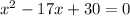
We now split the middle term to obtain;

`x^2-15x-2x+30=0`

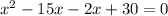
We factor to obtain;

`x(x-15)-2(x-15)=0`

`(x-15)(x-2)=0`

`(x-15)=0\:or\:(x-2)=0`

`x=15\:or\:x=2`

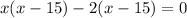
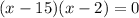
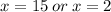
Therefore the correct answer is option C