Question

What value of k would make these inverses? M(x) = 6x^2 – 12 and M^-1 = √((x/3k)+k)

A.) k = -2
B.) k = 6
C.) k = 2
D.) k = 4

Answer 1

Option 2 - k=2

Explanation:

Given :
`M(x)=6x^2-12` and
`M^(-1)= \sqrt{(x)/(3k)+k}`

To find : What value of k would make these inverses?

Solution :

First we find the inverse of M(x)

Let,
`y=6x^2-12`

Interchange x and y,

`x=6y^2-12`

Now, find the value of y

`x+12=6y^2`

`(x+12)/(6)=y^2`

Taking root both side,

`y=\sqrt{(x+12)/(6)}`

`y=\sqrt{(x)/(6)+(12)/(6)}`

`y=\sqrt{(x)/(6)+2}`

`M^(-1)=\sqrt{(x)/(6)+2}`

Now, we compare or equate both the inverse function.

`\sqrt{(x)/(6)+2}= \sqrt{(x)/(3k)+k}`

`\sqrt{(x)/(3(2))+2}= \sqrt{(x)/(3k)+k}`

On caparison the value of k=2.

Therefore, Option C is correct.

Answer 2

We are given function:
`M(x) = 6x^2-12.`

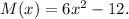
Let us find it's inverse.

In order to find it's inverse, we need to get function equal to y.

`y= 6x^2-12`

Switching x and y's .

`x= 6y^2-12`

Now, solving it for y.

`x+12 = 6y^2`

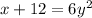
Dividing both sides by 6, we get

`y^2=(x)/(6) +(12)/(6)`

`y^2=(x)/(6) +2`

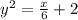
Taking square root on both sides, we get

`√(y^2) =\sqrt{(x)/(6) +2}`

`y=\sqrt{(x)/(6) +2}`

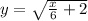
Re-writing in the form of given inverse.

`m^(-1)(x)=\sqrt{(x)/(3*2) +2}`

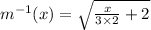
On comparing with given M^-1 = √((x/3k)+k).

`\sqrt{(x)/(3k)  +k} = \sqrt{(x)/(3*2) +2}`

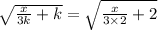
k=2.

Therefore, correct option is C.) k = 2.