Question

Chase has 3 gallons of a solution that is 30% antifeeze that he wants to use to winterize his car. How much pure antifreeze should he add to this solution to produce a solution that is 65% antifreeze.

Answer 1

Let x gallons be the amount of pure antifreeze that should be added to the 30% solution to produce a solution that is 65% antifreeze. Then the total amount of antifreeze solution will be x+3 gallons.

There are 30% of pure antifreeze in 3 gallons of solution, then

3 gallons - 100%,

a gallons - 30%,

where a gallons is the amount of pure antifreeze in given solution.

Mathematically,

`(3)/(a)=(100)/(30),\\ \\a=(3\cdot 30)/(100)=0.9\ gallons.`

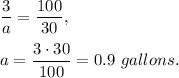
Now in new solution there will be x+0.9 gallons of pure antefreeze.

x+3 gallons - 100%,

x+0.9 - 65%

or

`(x+3)/(x+0.9)=(100)/(65),\\ \\65(x+3)=100(x+0.9),\\ \\65x+195=100x+90,\\ \\35x=105,\\ \\x=3\ gallons.`

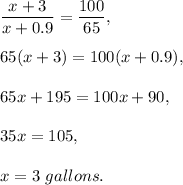
Answer: he should add 3 gallons of pure antifreeze.