Answer:
Sum of series is 40.
Explanation:
Given : Geometric series .
To find : Sum of geometric series.
Solution : We have given that ∑
 n = 1 to 4
n = 1 to 4
For n = 1
 =
=
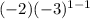
 = (-2)(1)
= (-2)(1)
 = -2.
= -2.
For n =2
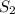 =
=
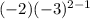 .
.
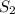 = 6.
= 6.
For n =3
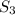 =
=
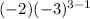 .
.
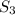 =
=
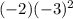 .
.
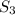 = (-2)(9).
= (-2)(9).
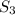 = -1.
= -1.
For n =4
 =
=
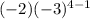 .
.
 =
=
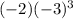 .
.
 =
=
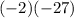 .
.
 = 54.
= 54.
Sum of all
 +
+
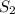 +
+
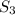 +
+
 .
.
-2 + 6 + (-18) + 54
-2 +6 -18 +54
4 -18+54
-14+54
40.
Therefore, Sum of series is 40.