Question

Find the 21st term of the geometric sequence that begins 2,6,18,54,...

Answer 1

21st term is 6973568802

Explanation:

2,6,18,54,...

nth term of geometric sequence is

`a_n= a_1(r)^(n-1)`

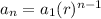
Where a1 is the first term and 'r' is the common ratio

a1= 2

To find common ratio , divide the second term by first term

`(6)/(2) =3`

`(18)/(6) =3`

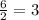
a1=2 and r= 3

`a_n= a_1(r)^(n-1)`

`a_n= 2(3)^(n-1)`

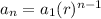
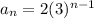
To find 21 term , replace n with 21

`a_(21)= 2(3)^(21-1)`

`a_(21)= 2(3)^(21-1)`

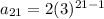
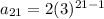
21st term is 6973568802

Answer 2

6973568802

Explanation:

I memorized the equation: A(n) = A(1)*d^(n-1).

You can plug into the equation A(21) = 2*3^20, which can be solved to 6973568802. (I solved this step through a calculator by finding 3^20, then multiplying that by 2 to get 6973568802.

Hope this helps!