Question

Hi guys I solved two inequalities but the answers are wrong and I would like you to help me with the results. The inequalities are the following:

x³-x²-4x+4<0
x^4-25x²+144<0

The x^4 is x raised to the fourth.

Answer 1

(1)
`x^3-x^2-4x+4<0`

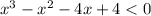
with this type of polynomials I first try to find one root by guess: it is 1. Then divide the polynomial by that root, (x-1), which quickly reveals the remaining roots:

`(x^3-x^2-4x+4)/(x-1)=x^2-4=(x-2)(x+2)`

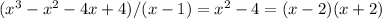
Se the cubic polynomial intersects the x axis in three points {-2,1,2}

Because the coefficient of the highest power (3) is positive and the power is odd, the expression is negative for x<-2, then it is positive until it crosses x again at x=1, then negative between 1 and 2, and finally becomes positive for x>2.

So the solutions are:

`x^3-x^2-4x+4<0\\(x+2)(x-1)(x-2)<0\implies -\infty < x<-2\,\,\,\mbox{and}\,\,\,1<x<2`

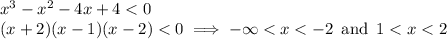
(2) In this case start with a substitution:
`z\leftarrow x^2`

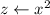
which will transform the quartic expression to a quadratic one:

`x^4-25x^2+144\rightarrow z^2-25z+144\implies z_1=16, z_2=9\\\implies x_(1,2)=\pm 4, \,\,x_(3,4)=\pm3\\(x+4)(x+3)(x-3)(x-4)<0`

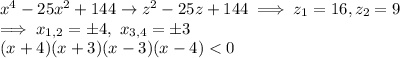
By a similar argument as with (1) you can determine the positive and negative regions. Since the highest power is even, the region x<-4 is in the positive, then crosses into negative for -4<x<-3, positive for -3<x<3, negative for 3<x<4, and finally positive for 4<x. So the solutions of the inequality are:

{-4<x<-3, 3<x<4}

Answer 2

The first answer is x<−2 or 1<x<2

and the second answer is −4<x<−3 or 3<x<4