here tension in the string is counter balanced by weight of block of mass m1
so we can say
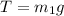
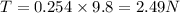
now on the other side the block which is placed on the inclined plane
we can say that component of weight of the block and friction force is counter balanced by tension force
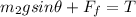
now we can plug in all values to find the friction force
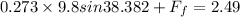
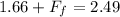
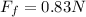
so it will have 0.83 N force on it due to friction
now to find the friction coefficient
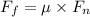
here we know that
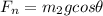
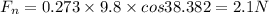
now from above equation
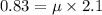
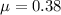
so friction coefficient will be 0.38