Answer:
The solution of the given equation is:
x=2 and x= -2
Explanation:
We are given an quadratic equation as:

Now we are asked to find the solution of this equation i.e. we are asked to find the possible value of x that satisfy this equation.
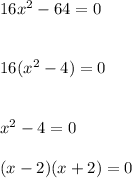
Since, we know that:
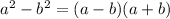
Hence, we have:
x=2 or x= -2
Hence, the solution of the equation are:
2 or -2.