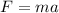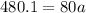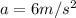here two forces are acting simultaneously
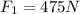 25^0 W of N
25^0 W of N
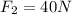 60^0 E of N
60^0 E of N
now we will write the two forces in components form
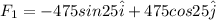
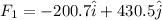
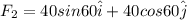
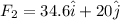
now net force on it will be
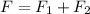
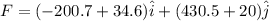
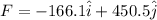
so net force is of magnitude
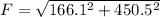
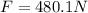
direction is given as
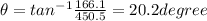
so net force is 480.1 N at 20.2 degree W of N
now the acceleration is given by Newton's II law