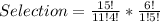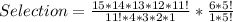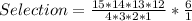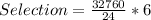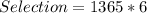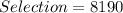Question

A committee must be formed with 5 teachers and 4 students. If there are 6 teachers to choose from, and 15 students, how many different ways could the committee be mad?

Answer 1

8190 ways

Explanation:

Given

`Teachers = 6`

`Students = 15`

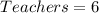
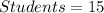
Selection

`Students = 4`

`Teachers = 5`

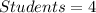
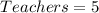
Required

Number of ways of selection

4 students can be selected from 15 students in:

`Students= ^(15)C_4`

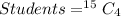
Similarly.

5 teachers can be selected from 6 teachers in:

`Teachers= ^(6)C_5`

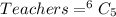
So, the required number of selection is:

`Selection = ^(15)C_4 * ^6C_5`

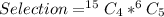
Apply combination formula:

`Selection = (15!)/((15-4)!4!) * (6!)/((6-5)!5!)`

`Selection = (15!)/(11!4!) * (6!)/(1!5!)`

`Selection = (15*14*13*12*11!)/(11!*4*3*2*1) * (6*5!)/(1*5!)`

`Selection = (15*14*13*12)/(4*3*2*1) * (6)/(1)`

`Selection = (32760)/(24) * 6`

`Selection = 1365 * 6`

`Selection = 8190`