Question

. (03.04 MC) The following is an incomplete paragraph proving that the opposite angles of parallelogram ABCD are congruent: Parallelogram ABCD is shown where segment AB is parallel to segment DC and segment BC is parallel to segment AD.

According to the given information, segment AB is parallel to segment DC and segment BC is parallel to segment AD . Using a straightedge, extend segment AB and place point P above point B. By the same reasoning, extend segment AD and place point T to the left of point A. Angles ______________ are congruent by the Alternate Interior Angles Theorem. Angles ______________ are congruent by the Corresponding Angles Theorem. By the Transitive Property of Equality, angles BCD and BAD are congruent. Angles ABC and BAT are congruent by the Alternate Interior Theorem. Angles BAT and CDA are congruent by the Corresponding Angles Theorem. By the Transitive Property of Equality,∠ ABC is congruent to∠ CDA. Consequently, opposite angles of parallelogram ABCD are congruent. What angles accurately complete the proof? (5 points) 1. BCD and CDA 2. CDA and BCD 1. BCD and PBC 2. PBC and BAD 1. PBC and CDA 2. CDA and BAD 1. PBC and BAT 2. BAT and BAD

Answer 1

The correct option is 2.

Explanation:

Given information: ABCD is a parallelogram, AB║DC, BC║AD.

It is given that segment AB is extended and place point P above point B and segment AD is extended and place point T to the left of point A.

Alternate Interior Angles Theorem: If a transversal line intersect two parallel lines then alternate interior angles are congruent.

`\angle 1\cong \angle 2` (Alternate Interior Angles Theorem)

`\angle BCD\cong \angle PBC` (Alternate Interior Angles Theorem)

The values of blank 1 is "BCD and PBC".

Corresponding Angles Theorem: If a transversal line intersect two parallel lines then corresponding angles are congruent.

`\angle 1\cong \angle 3` (Corresponding Angles Theorem)

`\angle PBC\cong \angle BAD` (Corresponding Angles Theorem)

The values of blank 2 is "PBC and BAD".

Using Transitive Property of Equality,

`\angle BCD\cong \angle BAD`

Similarly,

`\angle ABC\cong \angle BAT` (Alternate Interior Angles Theorem)

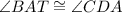`\angle BAT\cong \angle CDA` (Corresponding Angles Theorem)

Using Transitive Property of Equality,

`\angle ABC\cong \angle CDA`

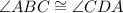
Consequently, opposite angles of parallelogram ABCD are congruent.

Therefore the correct option is 2.