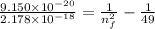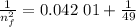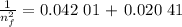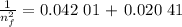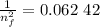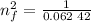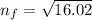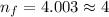Answer:
(n = 7) ⟶ (n = 4)
Explanation:
1. Convert the energy to joules per mole of electrons.
E = 55.1 × 1000 = 55 100 J/mol
2. Convert the energy to joules per electron
E = 55 100/(6.022 × 10²³)
E = 9.150 × 10⁻²⁰ J/electron
3. Use the Rydberg equation to calculate the transition
Rydberg's original formula was in terms of wavelengths, but we can rewrite it to have the units of energy. The formula then becomes
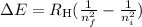
where
 = the Rydberg constant = 2.178 × 10⁻¹⁸ J
= the Rydberg constant = 2.178 × 10⁻¹⁸ J
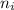 and
and
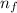 are the initial and final energy levels.
are the initial and final energy levels.