Question

Which of the following are solutions to the inequality -7x+14>-3x-6? Select all that apply.

-10
10
-5
5
-3
3
0

Answer 1

All real numbers less than 5 satisfy the inequality. The set of solutions of the inequality is the interval
`\left(-\infty \:,\:5\right)`.

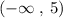Therefore, -10, -5, -3, 0, 3 are all valid solutions.

Explanation:

Solving an inequality means finding all of its solutions. A solution of an inequality is a number which when substituted for the variable makes the inequality a true statement.

To find all the solutions for the inequality
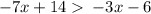`-7x+14>\:-3x-6` you must:

`\mathrm{Subtract\:}14\mathrm{\:from\:both\:sides}\\-7x+14-14>-3x-6-14`

`\mathrm{Simplify}\\-7x>-3x-20`

`\mathrm{Add\:}3x\mathrm{\:to\:both\:sides}\\-7x+3x>-3x-20+3x`

`\mathrm{Simplify}\\-4x>-20`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}\\\left(-4x\right)\left(-1\right)<\left(-20\right)\left(-1\right)`

`\mathrm{Simplify}\\\\4x<20\\\\(4x)/(4)<(20)/(4)\\\\x<5`

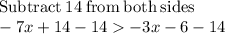
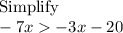
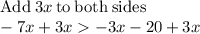
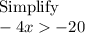
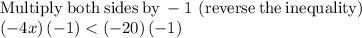
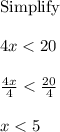
All real numbers less than 5 satisfy the inequality. The set of solutions of the inequality is the interval
`\left(-\infty \:,\:5\right)`.

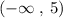Therefore, -10, -5, -3, 0, 3 are all valid solutions.

Answer 2

-7x+14>-3x-6

add 7x to each side

14> 4x-6

add 6 to each side

20>4x

divide by 4

5>x

x<5

solutions

3,0,-3,-5,-10