Consider ΔAQD. This triangle has the area
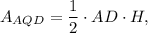
where H is the heigh drawn from the point Q to the side AD.
Note that the height H is also the height of the parallelogram. So the area of the parallelogram ABCD is

From these two statements you can conclude that

Now consider ΔDMQ. The ratio between the area of triangles DMQ and AQD is

Since
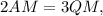 you have that
you have that
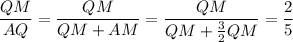
and
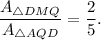
Thus,
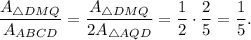
Answer: correct choice is B